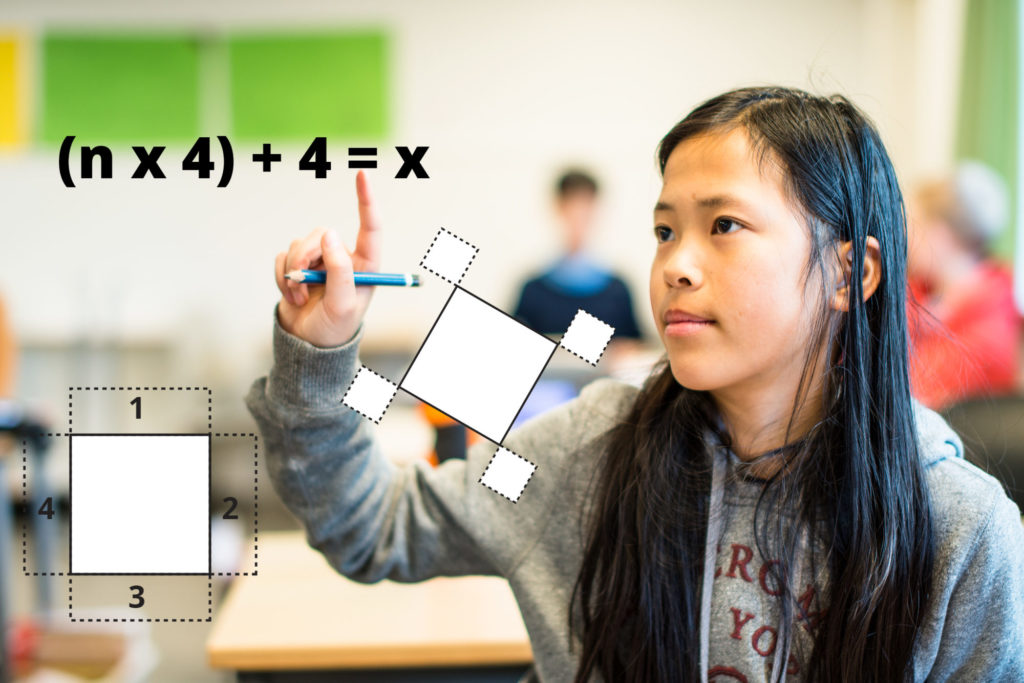
Tenkeskriving og presentasjonsskriving i matematikk
Skriving kan bidra til læring i matematikk og er samtidig ein viktig del av den matematiske kompetansen elevane skal utvikle.
Denne ressursen har vi utarbeidd i samarbeid med Matematikksenteret og viser korleis skriving kan inngå som ein naturleg del av matematikkfaget.
Kunnskapsløftet (LK20) framhevar at grunnleggjande ferdigheiter er avgjerande reiskap for læring, og dei skal bidra til utvikling av kompetansen til elevane i alle fag. I tillegg er grunnleggjande ferdigheiter ein del av kompetansen elevane skal utvikle i faga, og dei er integrerte i kompetansemåla på premissane til dei ulike faga. Å kunne skrive er ein av dei fem grunnleggjande ferdigheitene. Skriving kan bidra til læring i matematikk og er samtidig ein viktig del av den matematiske kompetansen elevane skal utvikle.
Å skrive i matematikk kan til dømes vere å:
- Bruke teikningar, diagram, tabellar og grafar (sjå til dømes Kadunz, 2007).
- Beskrive tankeprosessar (sjå til dømes Miller, 1991).
- Presentere framgangsmåter og resultat (sjå til dømes Flesher, 2003).
Hovudmålet med matematikkopplæringa i skulen er å utvikle den matematiske kompetansen til elevane. Kilpatrick og kollegaer (2001) beskriv matematisk kompetanse [1] ved hjelp av fem komponentar (sjå under). Å kunne skrive inngår i alle dei fem komponentane, til dømes:
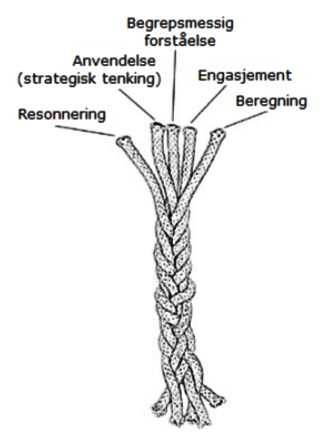
- Begrepsmessig forståelse:
Representere matematiske situasjoner på ulike måter. - Beregning:
Skriftlige prosedyrer. - Anvendelse:
Beskrive løsningsmetoder. - Resonnering:
Skriftlig argumentasjon og begrunnelse. - Engasjement:
Mestre skriftlig kommunikasjon.
Niss og Jensen (2002) definerer matematisk kompetanse ved hjelp av åtte kompetansar. Dei framhevar kommunikasjon som ein eigen kompetanse. Kommunikasjon i matematikk handlar om å kunne uttrykkje seg på forskjellige måtar, både skriftleg, munnleg og visuelt, for å gjere seg best mogleg forstått. Vidare handlar kommunikasjon om å uttrykkje seg på forskjellige nivå, med teoretisk og teknisk presisjon, om matematiske representasjonar. I møte med andre vil gradar av matematisk kompetanse variere og språket må derfor tilpassast kvar enkelt mottakar. Det teoretiske og tekniske nivået vil dermed vere avhengig av den matematiske kompetansen til mottakaren, der ein elev med høg matematisk kompetanse forstår ein representasjon på eit høgare nivå av teoretisk og teknisk presisjon enn ein elev med lågare matematisk kompetanse.
Vi ser at det å kunne skrive er viktig både i modellen til Kilpatrick m.fl. (2001) og modellen til Niss og Jensen (2002). Skriving er altså ein sentral del av den matematiske kompetansen til elevane, og i denne teksten vil vi beskrive to former for skriving i matematikk.

Tenkeskriving og presentasjonsskriving
Olga Dysthe, Frøydis Hertzberg og Torlaug Løkensgard Hoel (2000) har sett nærare på to former for skriving: tenkeskriving og presentasjonsskriving. Dei beskriv tenkeskriving som skriving for å lære, der skrivinga mellom anna handlar om å få fram idear og utforske og prøve ut tankar. Tenkeskrivinga blir dermed ein måte å få orden på og strukturere tankane og ideane for seg sjølv, og er ei form for skriving som alle kan meistre. Presentasjonsskriving blir forklart som fagskriving der fokuset er å lære å skrive. I motsetning til tenkeskriving, der skrivaren sjølv er mottakaren, blir presentasjonsskriving brukt for å kommunisere med ein lesar eller lyttar. Å skrive fagleg presist med riktig terminologi er eit viktig aspekt. Vidare i teksten vil vi beskrive korleis tenkeskriving og presentasjonsskriving kan bidra til å utvikle den matematiske kompetansen til elevane.
Tenkeskriving i matematikk
Når elevane bruker skriving for å utvikle forståing i matematikk, er skrivinga ei tydeleggjøring av tanken, og skrivinga blir slik ei støtte i tankeprosessen. Miller (1991) seier at fordi skriving leier oss til å tenke, vil omgrepsforståinga til elevane og ferdigheiter i matematikk bli styrka når dei blir utfordra til å skrive om kva dei har forstått. Denne forma for skriving kan sjåast på som tenkeskriving i matematikk. Til dømes kan elevar i arbeidet med å løyse eit matematisk problem ha behov for å strukturere informasjon, prøve ut ulike løysingsstrategiar, lage hjelpefigurar og gjere mellomrekningar. Alle oppgåver som inneber å ha oversyn med meir informasjon enn det elevane greier å halde styr på i hovudet, krev at elevane bruker skriving som verktøy i prosessen. I tillegg kan skriving i samband med utprøvingar av ulike strategiar, mellomrekningar og modellar bidra til at elevane får auge på samanhengar mellom representasjonar.
Eit døme på ei oppgåve i matematikk som gir elevane moglegheit til å tenkeskrive er oppgåva «Heller i hagen». Denne aktiviteten har mange namn og blir presentert i ulike former med ulike kontekstar. Til dømes omtaler Boaler og Humphreys (2005) oppgåva som «The boarder problem». Oppgåva går ut på at elevane blir presenterte for eit stort kvadrat som er delt inn i mange små kvadrat. Elevane skal finne ut kor mange kvadrat den ytterste rekka av kvadratet består av. Oppgåva kan løysast på mange ulike måtar.
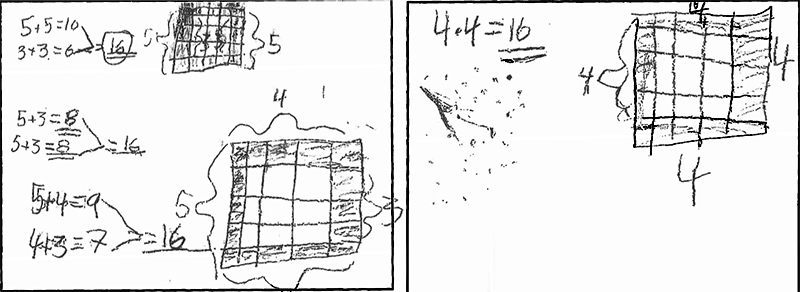
Illustrasjonen over viser korleis ein elev gjekk fram då han fekk i oppgåve å finne ut kor mange kvadrat det er i ramma på eit stort kvadrat som er delt inn i 25 små kvadrat. På bildet ser vi korleis eleven har brukt tre forskjellige strategiar for å løyse oppgåva. Vi ser at eleven har brukt både illustrasjonar og mellomrekningar. Vi veit ikkje om eleven har brukt illustrasjonane som ein del av strategien, eller om illustrasjonane er meint for å vise kva som er tenkt. Likevel får vi eit innblikk i dei matematiske ideane til eleven. Bruken av ulike representasjonar bidrar òg til å styrke omgrepsforståinga til eleven (Kilpatrick, 2001).
Eit anna døme på tenkeskriving kan vere skriving for å utvikle omgrepsforståing. Bildet under viser eit omgrepskart der ein elev har arbeidd med omgrepet firkant. Omgrepskartet består av fire ruter; definisjon, fakta, døme og motdøme. Etter at elevane har fylt ut rubrikkane definisjon og fakta i skjemaet, sit dei saman i grupper for å diskutere dei einskilde sine forklaringar og eventuelt justere desse forklaringane i etterkant. Elevane får deretter sjå ulike figurar og skal saman avgjere om figurane er firkantar eller ikkje, for så å plassere figurane under døme eller motdøme i skjemaet sitt. Etter kvart som det dukkar opp nye figurar, må elevane vurdere eigenskapane til figurane og avgjere om dei passar inn i forklaringa dei hadde laga seg på førehand. Etter kvart som stadig nye figurar dukkar opp, blir både forklaringane og elevane si forståing for firkantar utfordra. I løpet av denne prosessen stiller elevane gjerne spørsmål ved forklaringane sine, noko som kan resultere i ny forståing og meir presise forklaringar.

I dømet over blir skriving brukt til å forstå matematikk. Det er heilt klart behov for ulike former for forklaringar og representasjonar for å forstå kva som definerer ein firkant. Omgrepskartet kan bli brukt til å utvikle forståing for ulike omgrep. Skjemaet utfordrar elevane si forståing for omgrep dei arbeider med gjennom at definisjonar blir endra, og nye dømer, motdømer og fakta blir skrive inn. Aktiviteten er henta frå Metsisto, D. (2005) og omsatt til nynorsk.
Presentasjonsskriving i matematikk
Når elevene bruker skriving til å presentere en matematisk idé for en annen elev, blir måten det presenteres på avgjørende for om leseren kan ta del i denne idéen. Som tidligere nevnt, beskriver Niss og Jensen (2002) at kommunikasjonskompetanse i matematikk handler om å forstå og fortolke utsagn og tekster, og det handler om å uttrykke seg på forskjellige måter og på forskjellige nivåer. Kommunikasjon skjer mellom avsender og mottaker. Når elevene skal uttrykke seg, er det viktig at de kjenner til og kan bruke et riktig og presist fagspråk og tilpasse det slik at det blir forståelig for mottakeren. Å tilpasse språket til mottakere med lavere eller høyere faglig kompetanse er med på å utvikle skriverens forståelse av det aktuelle temaet (Niss & Jensen, 2002). En tilpasning av språket fører til refleksjon over egen tenkning fordi en skriftliggjøring eller muntlig verbalisering av et resonnement eller tankegang er kognitivt krevende. Skriveren blir tvunget til hele tiden å vurdere om det som blir skrevet faktisk underbygger egen tenkning. For å skrive til personer med høyere matematisk forståelse vil et mer presist språk med matematisk begrepsbruk være mer aktuelt. Skriveren reflekterer dermed over begrepenes betydning og får samtidig et nytt eksempel på en situasjon der begrepet kan brukes, som i sin tur beriker forståelsen for begrepet. For å skrive til personer med lavere matematisk forståelse, må språket forenkles på en slik måte at personen forstår hva som menes og samtidig passe på at innholdet ikke endres.

Når elevane bruker skriving til å presentere ein matematisk idé for ein annan elev, blir måten denne idéen blir presentert på, avgjerande for om lesaren kan ta del i denne idéen. Som tidlegare nemnt, forklarer Niss og Jensen (2002) at kommunikasjonskompetanse i matematikk handlar om å forstå og fortolke utsegn og tekstar, og det handlar om å uttrykke seg på forskjellige måtar og på forskjellige nivå. Kommunikasjon skjer mellom avsendar og mottakar. Når elevane skal uttrykkje seg, er det viktig at dei kjenner til og kan bruke eit riktig og presist fagspråk og tilpasse det slik at det blir forståeleg for mottakaren. Å tilpasse språket til mottakarar med lågare eller høgare fagleg kompetanse er med på å utvikle skrivaren si forståinga av det aktuelle temaet (Niss & Jensen, 2002). Ei tilpassing av språket fører til refleksjon over eigen tenking fordi ei skriftliggjøring eller munnleg verbalisering av eit resonnement er kognitivt krevjande. Skrivaren blir tvinga til heile tida å vurdere om det som blir skrive faktisk underbygger eigen tenking. Når eleven skal skrive til personar med høgare matematisk forståing enn han sjølv har, vil eit meir presist språk med matematisk omgrepsbruk vere meir aktuelt. Skrivaren reflekterer dermed over kva omgrepa betyr og får samtidig eit nytt døme på ein situasjon der omgrepet kan brukast, noko som i sin tur gjer forståinga for omgrepet endå rikare. For å skrive til personar med lågare matematisk forståing, må språket forenklast på ein slik måte at personen forstår kva som blir meint og samtidig passe på at innhaldet ikkje blir endra.
I dei fleste klasserom blir kommunikasjonskompetansen til elevane utvikla gjennom å aktivt ta i bruk det munnlege språket. Det kan skje gjennom aktivitetar som legg til rette for at elevane må diskutere og argumentere. Niss og Jensen (2002) peiker likevel på at det skriftlege språket òg er ein del av kommunikasjonskompetansen. Elevane treng trening i å kommunisere skriftleg og tilpasse seg nivået til mottakaren, slik at dei blir forstått. Ein aktivitet som legg til rette for at elevane får trene på skriftleg kommunikasjon, er ei vidareføring av oppgåva i dømet ovanfor, der elevane skulle finne talet på kvadrat i ytterramma av eit stort kvadrat.
Elevsvaret på bildet under viser korleis ein elev har forklart korleis han har tenkt når han kom fram til uttrykket . Presentasjonen til eleven består både av notasjon, figurar og tekst, og alle representasjonane er viktige for å kommunisere kva som er tenkt.

I arbeidet med slike presentasjonar får elevane trening i å argumentere og forklare tenkemåtar skriftleg. Samtidig får dei òg utvikla den matematiske kompetansen sin gjennom å tilpasse språket for ein bestemt mottakar, noko som gjer at dei må gå gjennom sin eigen tankegang fleire gonger. Det er likevel viktig at læraren ikkje stoppar her, men utfordrar elevane vidare til å gjere forklaringar og argumentasjonen betre og med eit meir presist fagspråk. I dømet over kan eleven til dømes få spørsmål om kva som er meint med «Hjørnene er 4 uansett figur». Sannsynlegvis meiner elevane talet på hjørne. Det kjem heller ikkje klart fram at n står for nummeret til figuren i rekka, og at kvar side i denne samanhengen er talet på steinheller på kvar side av det store kvadratet, sett bort frå dei fire hjørnesteinane. Vi ser at figurane er ei god støtte til teksten, men eleven kan framleis trene på å beskrive meir presist i verbalteksten. Ein måte å arbeide vidare med slike presentasjonstekstar på, er å la elevane lese andre elevar sine tekstar. Elevane kan gi tilbakemelding om kva dei forsto og kva som var vanskeleg å forstå.
I alle døma som er viste her, har elevane brukt ulike representasjonar, og det ønsker vi å framheve som ein viktig del av skriving i matematikk. Elevar får tilgang til dei matematiske ideane til andre elevar berre gjennom representasjonane deira av idéane fordi matematikken av natur er abstrakt. Kor djup forståinga er, blir relatert til kor sterkt representasjonane til elevane er knytt til kvarandre (NCTM, 2014). Gjennom ein aktiv bruk av både tenkeskriving og presentasjonsskriving, vil elevane sitt repertoar, bruk og forståing av ulike representasjonar bli styrkt.
Referansar
- Boaler, J., & Humphreys, C. (2005). Connecting mathematical ideas: Middle school video cases to support teaching and learning (Vol. 1). Heinemann Educational Books.
- Flesher, T. (2003). Writing to learn in mathematics. The WAC Journal, 14, 37-48.
- Kilpatrick, J., Swafford, J., & Findell, B. (2001). Adding it up. Mathematics Learning Study Committee, Center for Education, Washington, DC: National Academy Press.
- Kadunz, G. (2007) MATHEMATICAL WRITING. WORKING GROUP 1. The role of images and metaphors in the learning and understanding mathematics 83, 131.
- Metsisto, D. (2005). Reading in the mathematics classroom. Hentet 11. april 2016, fra: http://www.ascd.org/publications/books/105137/chapters/Reading-in-the-Mathematics-Classroom.aspx
- Miller, D. (1991). The mathematics teacher. Vol. 84 No. 7. pp. 516-521.
- National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all.
- Niss, M., & Jensen, T. H. (2002). Kompetencer og matematiklæring: Ideer og inspiration til udvikling av matematikundervisning i Danmark. København: Undervisningsministeriet.OECD. (2013) PISA 2012 Assessment and Analytical framework: Mathematics, Reading, Science,Problem Solving and Financial Literacy.
- [1] Norsk oversettelse av Kilpatrick, Swafford & Findell (2001) sin definisjon av mathematical proficiency.

